Chapter7 PBR(物理ベースレンダリング)
PBR
PS4辺りからトレンドになった技術。
処理能力向上により、Phongの反射モデルでは取り入れられなかった物理的に正しいライティングができるようになった。
以下を満たすことで物理的に正しい処理になる。
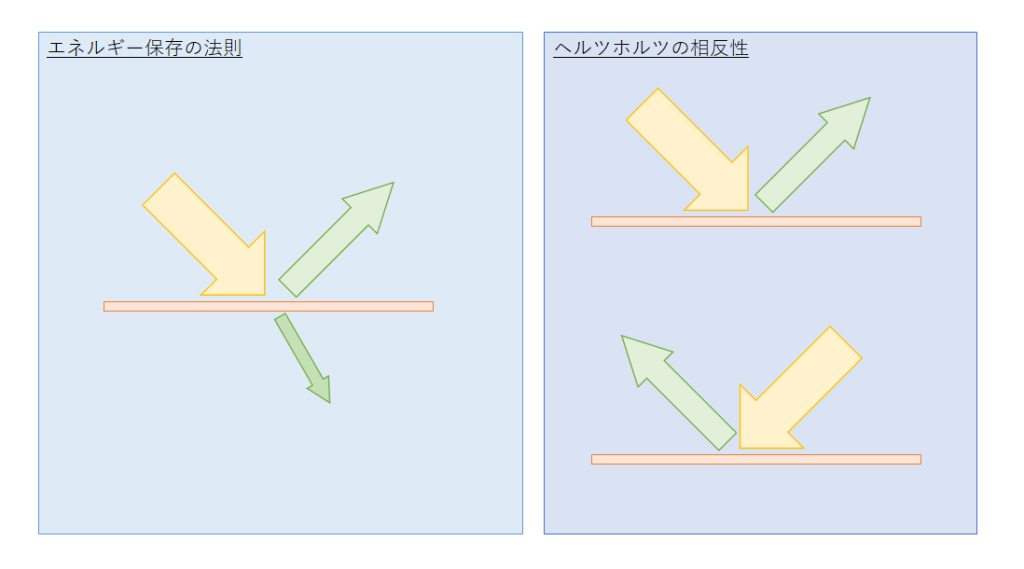
- エネルギー保存の法則
→ 入射光より強い光を跳ね返さないこと(入射光の一部を吸収し反射する) - ヘルツホルツの相反性
→ 入射方向と射出方向が入れ替わっても射出量が変化しない
Phongの反射モデルはエネルギー保存の法則を満たしていないためPBRではない。
正規化Lambert拡散反射
Lambert拡散反射によるエネルギー総量を積分すると入射エネルギーのπ倍になる。
よってこれではエネルギー保存の法則が満たせない。
Lambert拡散反射の計算結果にπを除算することでエネルギー保存の法則を満たしPBRなライティングになる。
この、πで除算した拡散反射の計算モデルを正規化Lambert拡散反射という。
diffuse /= 3.1415926f;左が除算前、右が除算後

ディズニーの論文によるPBR
ディズニーの論文(Physically Based Shading at Disney)
https://media.disneyanimation.com/uploads/production/publication_asset/48/asset/s2012_pbs_disney_brdf_notes_v3.pdf
元々ラプンツェルの髪の表現で作ったけど、
服などその他の部分はPBRじゃないから沢山ライティングいるし髪と大幅に反射が違うから不自然だし不便だよねってことで全部PBRのシェーダーが進んでいったらしい。
とにかくこの論文が今のPBRのベースになってるらしい。
パラメーター
物理的なパラメーターを調整することで多くの表現ができることを目的としている。
元が映画制作のためというのもあり、
映像を作成するのに効果的な、1個のカラー情報と10個のパラメーターに絞られた。
| パラメーター名 | 説明 |
|---|---|
| baseColor | サーフェイスカラー |
| subsurface | 表面化錯乱具合。 大きいほど拡散反射が起きる |
| metallic | 金属度 |
| specular | 鏡面反射率 |
| specularTing | スペキュラーカラーをベース色にするための調整値 |
| roufhness | 表面の粗さ |
| anistropic | 異方性反射率 |
| sheen | 光沢 |
| sheenTint | 光沢をベース色にするための調整値 |
| clearcoat | クリアコート |
| clearcoatGloss | クリアコートの光沢の調整値 |
割とBlenderのBRDFそのままって感じ。
ゲーム使用のPBRで使われるパラメータ
アルベドカラー
これまで使用していたテクスチャはディフューズテクスチャ。
PBRで使用するテクスチャはアルベドテクスチャ。
違いはライティング結果による陰影が描かれているかどうか。
ディフューズは陰影を描かれているため、そのまま使っても陰影があった。
アルベドは陰影を描いてはいけないため、そのまま使うとのっぺりする。
サーフェイスカラー(baseColor)に該当。
スペキュラーカラー
鏡面反射用のテクスチャ。
アルベドと同義で扱われる。
稀に分かれてる。
その際はアルベドカラーの方にブラーがかかってる。
(拡散反射光は物体内部で拡散して反射するため)
baseColor = サーフェイスカラー = アルベドカラー = スペキュラーカラー と覚えておけばひとまず大丈夫。
メタリック
鏡面反射光の色を物体のカラーか光源のカラーどちらの割合を多くするかの設定。
金属は物体の色を返すが、非金属は光源の色を返すため。
粗さ
物体表面の目に見えない小さな凹凸を表す。
レンダリングエンジンによって粗さ(roughness)、マイクロサーフェイス、滑らかさ(smooth)など名称が変わるが意味は一緒。
※ Unityでは滑らかさ、UE4では粗さ
ワークフロー
使用するエンジンによりPBRのパラメータからテクスチャの作り方まで変わってくる。
PBRだからこう!というわけではなく、エンジンのワークフローに従うことが大事。
実装
ディズニーの論文をベースにした今回独自のPBRを組む。
- 拡散反射: 正規化Lambert拡散反射 + フレネル拡散反射
- 鏡面反射: Cook-Torranceモデル
- ワークフロー: Unityメタリックモード(アルベドカラー、メタリック、滑らかさで表現)
メタリックマップはワークフローの関係でrにメタリック、aに滑らかさが格納されてる
// step-1 各種マップにアクセスするための変数を追加
// アルベドマップ
Texture2D<float4> g_albedo : register(t0);
// 法線マップ
Texture2D<float4> g_normalMap : register(t1);
// メタリックマップ
Texture2D<float4> g_metallicSoothMap : register(t2);前述の通り、正規化Lambert拡散反射とフレネル拡散反射を求め、それをアルベドに混ぜて拡散反射光とする。
※ フレネル拡散反射の詳細については後述
// step-3 シンプルなディズニーベースの拡散反射を実装する
DirectionalLight light = directionalLight[ligNo];
// フレネル拡散反射を算出
float diffuseFromFresnel = CalcDiffuseFromFresnel(normal, -light.direction, toEye);
// 正規化Lambert拡散反射を算出
float NdotL = saturate(dot(normal, -light.direction));
float3 lambertDiffuse = light.color * NdotL / PI;
// 拡散反射を合成
float diffuse = albedoColor * diffuseFromFresnel * lambertDiffuse;Cool-Torranceについては詳細を割愛。
メタリックは金属である割合のため、これを利用し金属と非金属それぞれの反射を表現する。
※ specColor = アルベドカラー
- 金属: 色が付く
- 非金属: 色が付かず白っぽくなる
// step-5 Cook-Torranceモデルを利用した鏡面反射率を計算する
float3 spec = CookTorranceSpecular(-light.direction, toEye, normal, smooth) * light.color;
spec *= lerp(float3(1.0f, 1.0f, 1.0f), specColor, metallic);滑らかさが高いほど拡散反射が弱くなる。
// step-6 滑らかさを使って、拡散反射光と鏡面反射光を合成する
lig += diffuse * (1.0f - smooth) + spec;
PBRと言ってもワークフローでかなり変わるみたい。
今回のだとUEとUnityの中間くらいな印象?
実はUnityBRPもURPもHDRPも全部PBR。
ただワークフローやレンダーパイプラインの違いによってあれだけの見た目の差が生じているだけで、基本原理は同じ。
今回のフレネル拡散反射
今回の実装は「フレネル反射率が低い時に拡散反射率が高くなる」という箇所に着目した簡易式で表現。
本来の計算式は更に後述で記載。
フレネル反射は鏡面反射のこと。
光の入射角が大きい(面に対して水平な)ほど鏡面反射率が上がる
エネルギー保存の法則に則り、光の総量は拡散反射量 + 鏡面反射量であることを考えると、
光の入射角が小さい(面に対して垂直な)ほど拡散反射率が上がる と言える。
更に、実際に目に入る光(カメラの位置)を考慮すると、
「光の入射ベクトル」「法線ベクトル」「カメラまでのベクトル」のなす角が小さい程強いと言える。
float CalcDiffuseFromFresnel(float3 N, float3 L, float3 V)
{
// step-4 フレネル反射を考慮した拡散反射光を求める
float dotNL = saturate(dot(N, L));
float dotNV = saturate(dot(N, V));
return dotNL * dotNV;
}実際のフレネル拡散反射
\( f_d = \frac{\text{baseColor}}{\pi} \left(1 + (F_{D90} – 1) (1 – \cos\theta_{l})^5 \right) \left(1 + (F_{D90} – 1)(1 – \cos\theta_{v})^5 \right) \)
ただし、光が面に対しほぼ平行に入射してきたときの拡散反射率を \( F_{D90} = 0.5 + 2 \times {roughness} \times \cos^2\theta_{d} \) とする。
ここで、それぞれ以下に分解できる。
- アルベドカラー: \( \frac{\text{baseColor}}{\pi} \)
正規化するためπで割る。 - 法線と入射光ベクトルとの拡散反射率: \( \left(1 + (F_{D90} – 1) (1 – \cos\theta_{l})^5 \right) \)
- 法線とカメラベクトルとの拡散反射率: \( \left(1 + (F_{D90} – 1)(1 – \cos\theta_{v})^5 \right) \)
今回使用した式は以下。
Nはベクトル、Lは入射光ベクトル、Vはカメラべクトルを示す。
(dotは内積を求める関数として省略)
\( f_d = \frac{\text{baseColor}}{\pi} \left(dot(N, L)\right) \left(dot(N, V)\right) \)
法線と入射光・カメラベクトルの拡散反射率の詳細
法線と入射光の式を基準に考える。
\( \left(1 + (F_{D90} – 1) (1 – \cos\theta_{l})^5 \right) \)
一番左の1とその次の1は、垂直入射した際の拡散反射率(100%の意)。
\( F_{D90} \) は、平行入射した際の拡散反射率。
基本的に1より小さくなる。
そのため \( (F_{D90} – 1) \) は基本的にマイナスになる。
\( (1 – \cos\theta_{l}) \) は、法線と光源に向かうベクトルの内積。
5乗してる理由はカーブをつけるため。
(現実世界の現象は指数関数的な変化をするため)
カメラの場合はこれがカメラに向かうベクトルに変わるだけ。
この式を実装に変換すると以下のようになる。
// 垂直入射した時の拡散反射率 (一番左の1)
float f0 = 1.0f;
// 平行入射した時の拡散反射率 (Fd90 - 1の結果)
float f90 = 0.5f;
// 法線との内積
float t = pow(1.0f - dot(N, L), 5.0f);
// 拡散反射の算出
flaot diffuseRate = lerp(0f, 90f, t);結局何してたかというと、
垂直反射率と平行反射率とのバランスを、法線との内積を利用して算出しているということ。
この言葉が最初にあればすんなり理解できたのに…()
Fd90について
光が面に対しほぼ平行に入射してきたときの拡散反射率
\( F_{D90} = 0.5 + 2 \times {roughness} \times \cos^2\theta_{d} \)
基本1より小さい値になると前述したが、最大で2.5になるらしい。
そりゃそうで、roughnessは0~1, cos2θも0~1なのだから、
0.5 + 2 * 1 * 1 で 2.5になるね。
だから範囲は 0.5 ~ 2.5 となる。
これにより、面が粗さを考慮した拡散反射を求めることができる。
実装
ディズニーの論文からの式ではエネルギー保存の法則が満たされていないことがあるが、
これを解消するEA DICEによる改良版コードを使用する。
float CalcDiffuseFromFresnel(float3 N, float3 L, float3 V)
{
// step-1 ディズニーベースのフレネル反射による拡散反射を真面目に実装する。
// 光源へのベクトルと視線へのベクトルのハーフベクトル
float3 H = normalize(L + V);
// 粗さ
float roughness = 0.5f;
float energyBias = lerp(0.0f, 0.5f, roughness);
float energyFactor = lerp(1.0f, 1.0f / 1.51f, roughness);
// Fd90の算出
float dotLH = saturate(dot(L, H));
float Fd90 = energyBias + 2.0f * roughness * dotLH * dotLH;
// 法線と光源との拡散反射
float dotNL = saturate(dot(N, L));
float FL = (1 + (Fd90 - 1) * pow(1 - dotNL, 5));
// 法線と視線との拡散反射
float dotNV = saturate(dot(N, V));
float FV = (1 + (Fd90 - 1) * pow(1 - dotNV, 5));
return FL * FV * energyFactor;
}今回版

実際版

…わ、わからん!!
けどフレネル反射が強い位置の面でも拡散反射が強く出てるらしい。
EA DICEの改良版コードについて
DICE 論文「Moving Frostbite to PBR」および GDC 等で発表された、“Frostbite Disney Diffuse” モデルで使用される式。
float FD90 = 0.5 + 2.0 * roughness * dot(h, l) * dot(h, l);
float3 diffuse = baseColor / PI * (1.0 + (FD90 - 1.0) * pow(1.0 - dot(l, n), 5.0));数式にするとこう。
〇 ディズニーの論文から導出される式
\( f_d = \frac{\text{baseColor}}{\pi} \left(1 + (F_{D90} – 1) (1 – \cos\theta_{l})^5 \right) \left(1 + (F_{D90} – 1)(1 – \cos\theta_{v})^5 \right) \)
\( F_{D90} = 0.5 + 2 \times {roughness} \times \cos^2\theta_{d} \)
〇 EA DICEの改良版
\( f_d = \frac{\text{baseColor}}{\pi} \left(1 + (F_{D90} – 1) (1 – \cos\theta_{l})^5 \right) \)
\( F_{D90} = 0.5 + 2 \times {roughness} \times \cos^2\theta_{h} \)
\( \left(1 + (F_{D90} – 1)(1 – \cos\theta_{v})^5 \right) \) は処理に対し得られる効果が少ないため省略。
Fd90で使用するcos2θがハーフベクトルに変わっている。
調べる感じ、元は \( F_{D90} = 0.5 + 2 \times {roughness} \) らしい、、
これ以上は論文読まないといけなくなるからここで撤退。
基本はEA DICE使っておけば良いと思う。



コメント