【HLSLシェーダーの魔導書】ライティング（Chapter5）のメモ

Chapter5 ライティング発展

ポイントライト

ディレクショナルライトと比べ、考慮しないといけない点は以下

入射してくる光の方向
光源との距離による光の減衰

入射光の方向

各頂点毎に入射方向を求める必要がある。

純粋に頂点と光源とのベクトルで良い。
　→ 頂点座標 – 光源座標

距離による減衰

距離は前述のベクトルの長さが該当する。

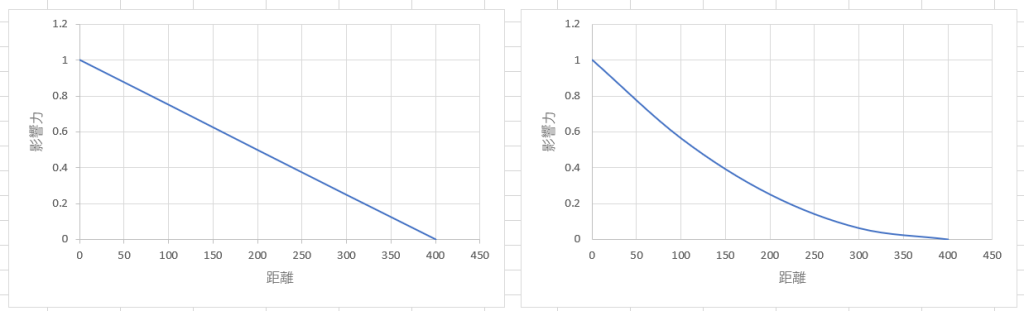
距離をD, 影響範囲をRとした時、頂点毎の影響力Aは以下で求まる。

A = 1 - (1 / R) * D [%]

※ 影響範囲はポイントライトの光の強さのイメージ。
ただし、このまま結果を使用すると距離と影響力が比例してしまい非現実的になるため、
影響力を2乗した値を使用し、緩やかになカーブにする。

実装

今回はディレクショナルライトと同様のモデルで実装する。

フローは以下。

光源座標と頂点座標から入射光のベクトルを算出
入射光ベクトルを使用し、拡散反射光、鏡面反射光を求める
入射光ベクトルの長さから影響力を求める
影響力を反射光に乗算し、最終的な反射光を算出する

cpp側

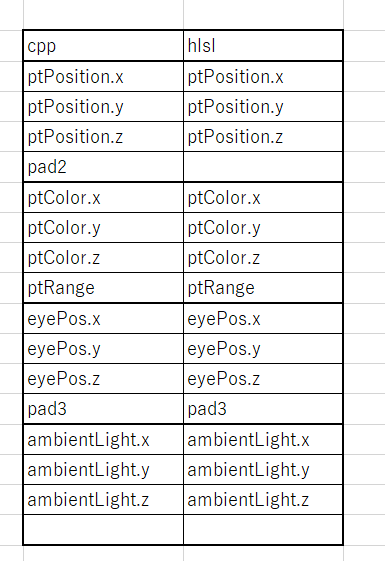
構造体を作る。

ptColorの次のfloatに必要な変数を入れているが、パディングじゃなくていい理由はなに？
　→ （後述で説明）

// step-1 ライト構造体にポイントライト用のメンバ変数を追加する
Vector3 ptPosition;     // ポイントライトの位置
float pad2;
Vector3 ptColor;        // ポイントライトのカラー
float ptRange;          // 影響範囲

hlsl側

拡散反射光、鏡面反射光を算出する処理は関数化しておくと便利。

// step-8 減衰なしのLambert拡散反射光を計算する
float3 diffPoint = CalcLambertDiffuse(ligDir, ptColor, psIn.normal);

// step-9 減衰なしのPhong鏡面反射光を計算する
float3 specPoint = CalcPhongSpecular(ligDir, ptColor, psIn.worldPos, psIn.normal);

動かすとちゃんとポイントライトしてることが見える。

構造体定義にパディングがいらないことの調査

パディングを入れてみる。

// step-1 ライト構造体にポイントライト用のメンバ変数を追加する

Vector3 ptPosition;     // ポイントライトの位置
float pad2;
Vector3 ptColor;        // ポイントライトのカラー
float pad4;　// ☆ 追加
float ptRange;          // 影響範囲
Vector3 eyePos;         // 視点の位置
float pad3;
Vector3 ambientLight;   // アンビエントライト

色がおかしくなった。

なんでptColorの後のptRangeをパディングなしで取れるのだ？

これに関してパディングとcpp-hlsl間のデータ連携の前提を間違えて理解している。

Vector3の受け渡しにパディングが必要なのではなく、その本質はスロットを整理するためのもの。

基本的に、データはスロットを跨いで取得することはできない。

1スロットあたり16バイトで構成されている中で、
例えば以下のような構造体の場合、cpp側では連続したメモリにデータが格納される。

struct sample
{
    Vector3 a;
    Vector3 b;
}

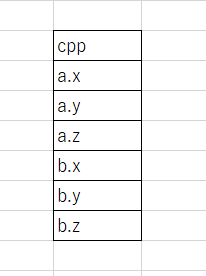
HLSLが1スロット(4バイト)ずつ読む際に、
float3 bの読み始めはb.xの位置(12バイト目)ではなく、次のスロットの16バイト目からになる。

だからデータがずれる。

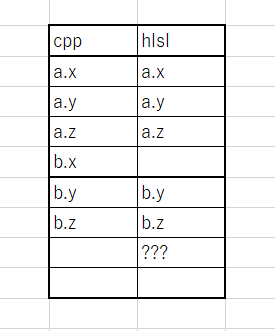
この、スロットの調整のためにパディングを設け、
スロットを跨ぐようなデータ配置になった時、次のスロットからデータが始まるようにするのがパディングの本質。

// step-1 ライト構造体にポイントライト用のメンバ変数を追加する
Vector3 ptPosition;     // ポイントライトの位置
float pad2;
Vector3 ptColor;        // ポイントライトのカラー
float pad4;　// ☆ 追加
float ptRange;          // 影響範囲
Vector3 eyePos;         // 視点の位置
float pad3;
Vector3 ambientLight;   // アンビエントライト

cbuffer DirectionLightCb : register(b1)
{
    // step-6 定数バッファーにポイントライト用の変数を追加
    float3 ptPosition;      // 位置
    float3 ptColor;         // カラー
    float ptRange;          // 影響範囲
    float3 eyePos;          // 視点の位置
    float3 ambientLight;    // アンビエントライト
};

今回の場合、pad4を追加したことで、pad4がHLSL側ptRangeとして読まれたためデータがずれた。

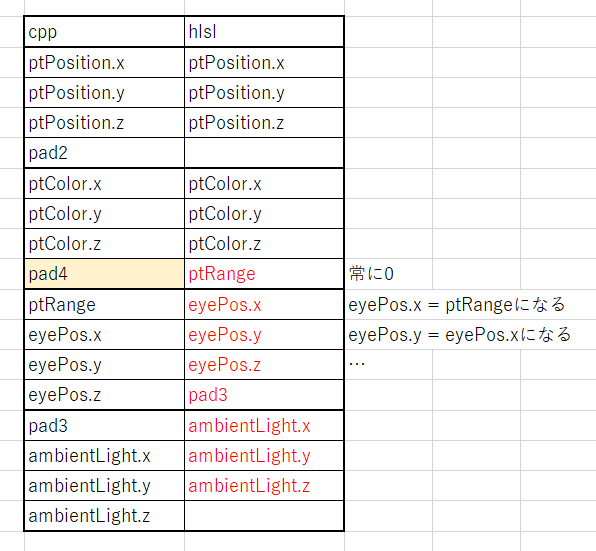
だからpad4は不要だった。

スポットライト

今回はコーンの表示はなし。残念。

実装はポイントライトのデータに放射方向と角度を追加するだけ。
処理手順は以下。

スポットライトの位置を光源として、ポイントライトを計算
そこから頂点へ向かうベクトルを計算
そのベクトルとスポットライトの放射方向ベクトルとの内積から角度を算出
その角度から影響率を算出

内積の特性

角度の算出には、内積のこの性質を利用する。

単位ベクトル同士の内積は、なす角の余弦の値になる

計算式は以下。

float angle = acos(dot(v1, v2));

内積の公式が a·b = |a||b|cosθ であることを考えると納得。

実装

// step-11 入射光と射出方向の角度を求める
float angle = abs(acos(dot(ligDir, spDirection)));

// step-12 角度による影響率を求める
affect = 1.0f - 1.0f / spAngle * angle;
if(affect < 0.0f) affect = 0.0f;
affect = pow(affect, 3.0f);

// step-13 角度による影響率を反射光に乗算して、影響を弱める
diffSpotLight *= affect;
specSpotLight *= affect;

step11は前述したとおり。absで符号を外す。
角度の影響率はポイントライトと同様の考え方。

wtf
思ったように光らない…

修正

after品を使ったら正常だったので何かが違う。

変数の型が違った。

// step-6 サーフェイスに入射するスポットライトの光の向きを計算する
float ligDir = normalize(psIn.worldPos - spPosition);
　↓
float3 ligDir = normalize(psIn.worldPos - spPosition);

これだとx成分しか残らず、以降float3として扱う時に{x, 0, 0}の状態になっていたっぽい。

これでもコンパイルエラーが出ないことが驚き…
C#ほど親切じゃないことに注意した方が良い。

コーン表示

せっかくなのでコーン表示に挑戦…
したかったが、3Dモデルを追加せず実装するには深度テクスチャが必須になる。

今のエンジンに深度テクスチャを取得するシステムがなく、かなり時間がかかりそうなので今はスキップ。
全部終わってからか、余裕ができたらやってみる。

リムライト

頂点法線と光の入射方向・視線方向を考える必要がある。

法線と入射方向

光の向きと頂点法線が垂直に近い箇所で強く光る。

これは、2つの単位ベクトルの内積となす角の関係が以下のようになる性質を利用して制御できる。

0°: 1.0
90°: 0.0
180°: -1.0

拡散反射光の演算とほぼ同様に影響度を制御できる。

拡散反射: 内積 * -1
　↓
リムライト: 1 - max(0, 内積)

法線と視線

入射方向と同様だが、方向が逆向きのため符号反転させる

1 - max(0, 内積 * -1)

ここまでの状況をまとめると下図のようになる。

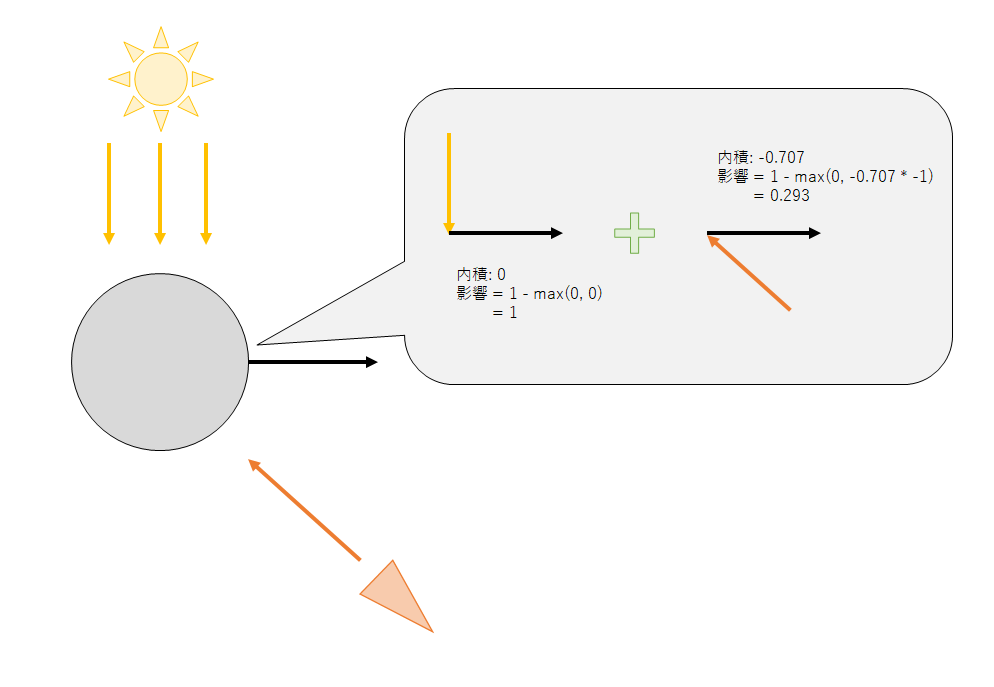
最終的にはこれらを乗算する。

実装

常にカメラを視線中央とするため、法線はカメラからの法線になるよう演算する。

SPSIn VSMain(SVSIn vsIn, uniform bool hasSkin)
{
    ...
    // step-2 カメラ空間の法線を求める
    psin.normalInView = mul(mView, psIn.normal);
    ...
}

カメラを視線中央にしている場合、視線ベクトルは(0, 0, 1)になる。
この場合、内積は常にz成分と同じ値になるため内積の計算は不要で、z成分を直接内積として扱える。

// step-4 サーフェイスの法線と視線の方向に依存するリムの強さを求める
float power2 = 1.0f - max(0.0f, psIn.normalInView.x * -1.0f)

結果

今までリムライトとかどうやって端の検出してたんだろうって思ってたけど、
法線との内積でやってたのは意外でびっくりした。

半球ライト

シンプルな計算だがディレクショナルライトよりリアルな光源。

PS3、スマホなどGPUの計算速度が心もとない環境で有効的。
今でもスマホゲーで採用されることがあるらしい（Unityにはなかったよね？）

考慮するのは地面の色（照り返しの色）と空の色の2種類。
計算は頂点法線と地面との内積を求めるだけ。
（ここまでくると内積だろうな～って予想がつくくらい内積大活躍）

計算

内積が1の場合は空、-1の場合は地面を向いていることになる。
それぞれ0~1に揃えるため、(内積 + 1) / 2 をする。

実装

空の色と地面の色の合成はLerpで良い。

float3 hemiLight = lerp(groundColor, skyColor, t);

左が地面の色、右が空の色の設定値。

light.groundColor = { 0.7f, 0.5f, 0.3f };
light.skyColor = { 0.15f, 0.7f, 0.95f };

結果

おそらく他のライトとか元のモデルの色に影響を受けて緑っぽくなってる。

実際には空の模様とか地面の模様とかで変わってくるだろうけれど、
最低限の処理であればここまでになる。

＼最新情報をチェック／