【HLSLシェーダーの魔導書】ライティング（Chapter4）のメモ

HLSL魔導士になる

Chapter4 ライティング基礎

ライトの種類

ディレクションライト

現実世界の太陽に近い存在。
位置、影響力の減衰が存在しない。
シンプルで高速。最も基本的なライト。

以下の要素で構成される。

  • 方向：3次元ベクトル
  • カラー：RGB

ポイントライト

位置と距離を考慮するライト。
複雑で処理も重い。

PS3, Xbox360辺りの時代だと1シーンに大量におけなかった。
　→ TBR系アルゴリズムによって大量配置が可能になった。

※ TBR系アルゴリズムはChapter16で紹介のため、そういうアルゴリズムによって変化があったことを覚えておく。

以下の要素で構成される。

  • 方向：3次元ベクトル
  • カラー：RGB
  • 影響範囲：メートル

影響範囲は光が届く距離の調整のための減衰率に関与する。

スポットライト

シンプルなものであればポイントライトを元に実装できる

以下の要素で構成される。

  • 方向：3次元ベクトル
  • カラー：RGB
  • 放射方向：3次元ベクトル
  • 放射角度：rad or deg（多分rad）
  • 影響範囲：メートル
スポットライトの各要素

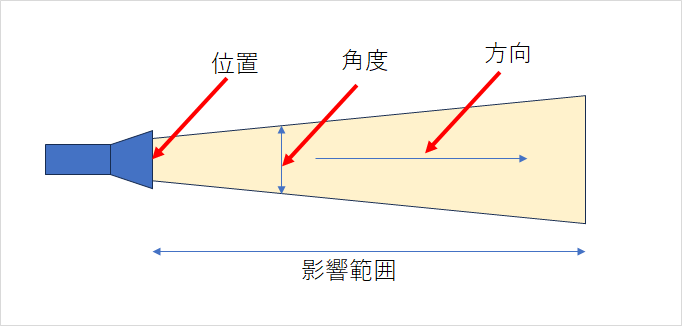
一時期スポットライトのコーンを表示するシェーダーを書こうとした時期があって結局書けなかったが、構成要素を知ることで何となく書けそうな気がしてくる。

反射モデル

ライトによる反射モデルはいくつかあり、今回はPhongの反射モデルを使用する。

反射モデルとは、

物体の表面がどのように光を反射するかを数値的に表現し、
コンピュータグラフィックスなどで視覚的な表現を可能にするためのモデルのこと。

光の入射方向と反射方向の間の関係を表す関数 (BRDF (Bidirectional Reflectance Distribution Function)) を用いて光の反射の特性を表現する。

Phongの反射モデルとは

Phongの反射モデル - Wikipedia
ja.wikipedia.org

ユタ大学の理学博士 ブイ・トゥオン・フォン により開発され、1973年に “Illumination for Computer Generated Pictures” という学位論文として発表された反射モデル。

同論文内で法線ベクトル補間手法も提案されており、Phongシェーディングとして知られている。
一番有名な反射モデルって覚えておけばよさそう。

その他の反射モデル

“Phongの” って言うことは他にもあるのか？
ということで調べてみた。

モデル名概要特徴用途
Blinn-PhongモデルPhongモデルの改良版。
Phongモデルと同様に非物理ベース。		スペキュラの計算にハーフベクトルを使う点が違う。軽量表現
Lambert反射モデル拡散反射の最も基本的なモデル。
Phongモデルの拡散反射と同一のモデル。		光の角度により強度が変わるが、観測方向に依存しない。非光沢表面（マット）
Cook-Torranceモデル物理ベースレンダリング(PBR)で使用される反射モデル。マイクロファセット理論に基づく。物理表現
Oren-NayarモデルLambertモデルの拡張。粗い拡散面を表現できる。ザラザラした物のリアルな拡散反射
Wardモデル表面の異方性を考慮したモデル。–金属など
DisneyBRDF
(Disney Principled BSDF)		Pixarが開発した反射モデル。多くのマテリアルを統一的に扱うことができ、Blenderで採用されている。PBR
Torrance-Sparrowモデル古典的なマイクロファセット理論を使用した反射モデル。Cook-Torranceと似ている。PBR?
Ashikhmin-Shirleyモデル異方性反射をリアルに表現したモデル。Wardより精度が高い。金属など？

…多っ！！

用途別にまとめると以下。

  • ゲームで軽量な表現: Phong、Blinn-Phong、Lambert
  • 映画・VFXなど高品質表現: Cook-Torrance、Disney BRDF
  • マットな材質: Oren–Nayar
  • 金属、光沢面: Cook-Torrance、Ward
  • 異方性素材(髪、布など): Ward、Ashikhmin–Shirley

こう見るとPhongが一番基本的な反射モデルに見える。
Phong自体も1973年とかなり前からあったのを考えると反射一つ取っても奥が深いことがよく分かる…

今回使用する反射モデル

Phong反射モデルは 拡散反射光、鏡面反射光、環境光 のそれぞれを合成したものになる。
今回は以下のように計算していく。

  • 拡散反射光 → Lambert拡散反射モデル
  • 鏡面反射光 → Phong鏡面反射モデル
  • 環境光 → 近似モデル

当然、各光要素を求める方法全てがPhongモデルに含まれているが、
今回は各要素ごとに別のモデルを使用する。

Lambert拡散反射光

光が当たっていれば明るく、当たっていなければ暗くするモデル。

計算は 法線とライト方向との内積 で行う。
※ 法線：面の向きを示す単位ベクトル

内積とは
【数学】「内積」の意味をグラフィカルに理解すると色々見えてくる - Qiita
線形代数の勉強を始めると割とすぐ出てきますよね、内積。計算自体はさほど難しくはないのだけれども、いまいちピンとこないという方、それなりにいるんじゃないでしょうか。私もそうでした。なので、今回の可…
qiita.com
 
a･b = (ax * bx) + (ay * by) ...
    = abcosθ

答えはスカラー（方向を持たない大きさのみのベクトル）になる。

単位ベクトル同士の場合、以下の性質がある。

  • 同じ向きの内積は1
  • 向きが異なるほど数値が小さくなり、逆向きになると-1

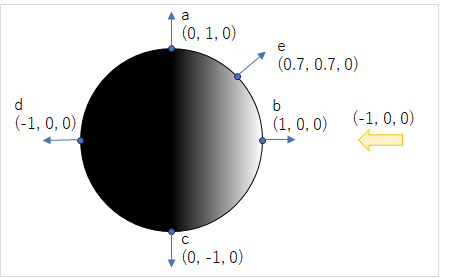
上図の様な関係の際、それぞれの内積は以下のようになる。

  • a: 0
  • b: -1
  • c: 0
  • d: 1
  • e: -0.7

この結果を全て-1すると、光（-1, 0, 0）により当たっている箇所が1に、当たっていない箇所が0以下になることが分かる。

  • a: 0   → 0     → 暗い
  • b: -1   → 1    → 明るい
  • c: 0 → 0    → 暗い
  • d: 1   → -1   → 暗い
  • e: -0.7 → 0.7 → やや明るい

つまり、Lambert反射モデルにおける反射光の求め方は

　法線と光の内積が1な程明るく、0な程暗くする

ということ。（単位ベクトルという前提）

cpp側

modelInitData.m_expandConstantBuffer = &directionLig;
modelInitData.m_expandConstantBufferSize = sizeof(DirectionalLight);

ディレクショナルライトもGPUで参照するため、定数バッファーを使用して渡す。
CPU側ではモデルデータ、シェーダーパス、ライトデータ（方向と強さ）を渡すだけで、
実際の陰影計算はGPU側で行う。

Vector3とfloat3の扱いについて

今回のディレクショナルライトは方向と色のデータをVector3で送っている。
その際に定義した構造体は以下。

struct DirectionalLight
{
    Vector3 ligDirection;
    float pad;
    Vector3 ligColor;
};

HLSL側で定義した定数バッファーは以下。

cbuffer DirectionLightCb : register(b1)
{
    float3 ligDirection;
    float3 ligColor;
};

この、cpp側で定義していたpadはパディングという、意図した変数である。

HLSLでは、定数バッファーのデータは16の倍数のアドレスに配置される。
対して、cppでは4の倍数のアドレスに配置されていく。

すると下図左側の表のように、2つ目の変数からcppとhlslでデータの不整合が起きる。

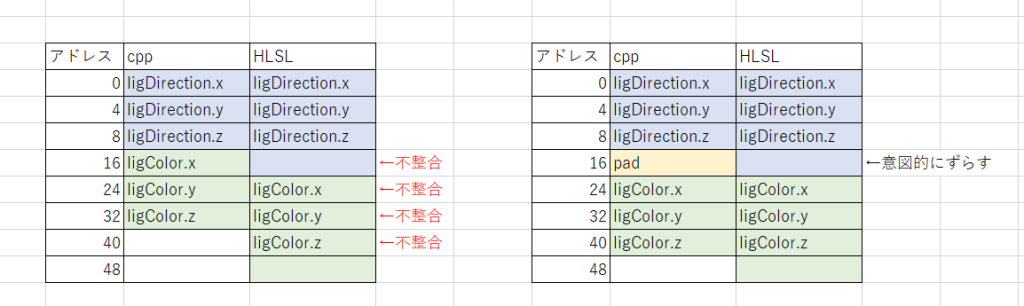
ここで、cpp側に2つめのVector3変数の前にfloat変数を挟むと4バイト分ずれるため
hlslとの不整合が起きなくなる。（上図右側の表）

UnityなどでHLSLを触る場合は意識しなくていいはずなので知識程度かな。
もし自分でcpp側を組むことがあれば覚えておくと過去の自分にとても感謝しそうな内容。

頂点法線の補正

SPSIn VSMain(SVSIn vsIn, uniform bool hasSkin)
{
    SPSIn psIn;

    // step-6 頂点法線をピクセルシェーダーに渡す
    psIn.normal = mul(mWorld, vsIn.normal);
}

モデルの回転に合うようにするには、頂点毎の法線にワールド行列を掛けることが必要。
頂点座標の配置空間を直す際もワールド行列を掛けたが、今回は回転を直すために掛けている。
　→ なんでこれで回転が直る？

法線は座標を無視し、回転と拡大だけで十分であるため、
ワールド行列を掛けることで位置、回転、拡大をまとめてワールド空間に直している。

なお、拡大については(1.0, 1.0, 1.0)である前提のため無視できる。
この通りでない場合（非等方スケーリング）は別途計算が必要。

反射光の演算

// step-7 ピクセルの法線とライトの方向の内積を計算する
float t = dot(psIn.normal, ligDirection);
t *= -1.0f; // 符号反転

dotで内積を求めることができる。
反射光から色を算出し、テクスチャカラーの乗算することで反射を組み込むことができる。

鏡面反射光 (Phongモデル)

金属のような反射を表現するためのモデル。
「反射した光がどれだけ目に飛び込んでくるか」を計算する。
　→ 屈折率を考慮した反射光って理解でいいと思う。

鏡面反射の強さに必要な処理

  • ライトが面に反射したベクトルを算出
  • 面から視点に向かって伸びるベクトルを算出
  • 上記2ベクトルの内積を算出 (これが鏡面反射の強さ)
  • 上記の値を絞り、最終的な反射値を算出

反射ベクトルの演算

光源ベクトルL、法線Nとした時の反射ベクトルRは以下で求まる。

R = L + 2(-N･L)N

これはHLSLのreflect関数の内部処理であり、通常はこのメソッドを使用すれば良い。

視点へのベクトルの演算

視点座標から光が入射した座標を引いた値。
入射した座標から視点座標へ移動すると考えると自然な式。
求めた値は正規化するのがベター。

反射ベクトルと視点へのベクトルとの内積

ここまで下図のような状態

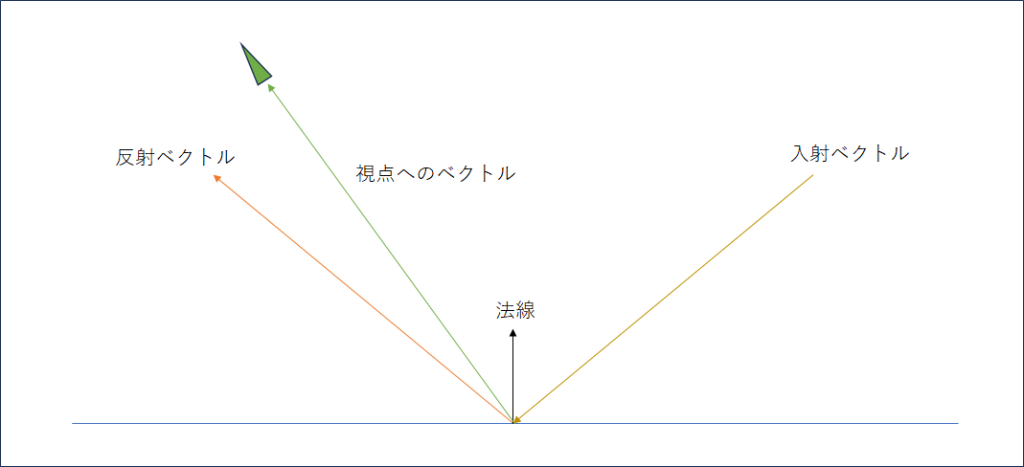
当然、光は視点に届いて初めて明るさとして認識されるため、
内積、つまりどの程度反射ベクトルが視点ベクトルと重なるかを求めれば
その値をもって反射値を算出できることは理解できる。

そういえば反射ベクトルはreflectで勝手に正規化されるって理解でいいのかな？
それとも法線が単位ベクトルって前提だから？
　→ 法線、光源ベクトル共に正規化されてる前提っぽい。

反射値の絞り

反射値を累乗して絞りを付けて行く。

累乗することで1未満の値を減少させることができ、
きれいな反射(1の値)以外の強さを調整できる。

定数バッファーの別の書き方

拡散反射の時もしれっと出ていたが、
定数バッファーは以下みたいにも書けるらしい。

// 今まで
flaot3 pos : register(b1)

// ☆ 別の書き方
cbuffer DirectionLightCb : register(b1)
{
    float3 ligDirection;
    float3 ligColor;
    float3 eyePos;
};

絞りの実装について

絞りの指数は5
大きいほど減衰が増す。

// step-7 鏡面反射の強さを絞る
t = pow(t, 5.0f);

実際は調整できるように変数化した方が良い気がする。
（今回はなんとなく5になってると思う。）

試しに2にしてみる。

想定通り僅かに明るい部分が増えた。

環境光

地面・壁などの跳ね返りの光(2次反射)などの間接光を加える。
ただし一般に2次反射の計算は対象が多く膨大になりパフォーマンスに大きく影響が出てくる。
　→ 物体は一律で同じ間接光を受けている として計算する。

この近似計算モデルを環境光(アンビエントライト)という。

rgb全てに一定の値を加算して底上げする。

実装

拡散反射と鏡面反射を足した光に対し、一律な値を加算するだけ。

// 拡散反射光と鏡面反射光を足し算して、最終的な光を求める
float3 lig = diffuseLig + specularLig;

// step-1 ライトの効果を一律で底上げする
lig.x += 0.3f;
lig.y += 0.3f;
lig.z += 0.3f;

一律で加算するアンビエント値は定数バッファーでcpp側から渡してもOK
エンジン固定ならこっちの方が編集しやすいかも？

float3 ambientLight : register(b1)

// step-9 拡散反射光と鏡面反射光を足し算して、最終的な光を求める
float3 lig = diffuseLig + specularLig + ambientLight;

＼ 最新情報をチェック ／

コメント

PAGE TOP
タイトルとURLをコピーしました