【HLSLシェーダーの魔導書】ライティング（Chapter6）のメモ

HLSL魔導士になる

Chapter6 さまざまなテクスチャの利用

テクスチャ

テクスチャの種類は以下のようなものがある。

  • ディフューズマップ: 模様を表現する（一般にテクスチャって言われたらこれ）
  • 法線マップ: 凹凸を表現する
  • ハイトマップ: 高さを表現する
  • 透明度マップ: 透明度を表現する
  • スペキュラマップ: 鏡面反射を表現する
  • AO(アンビエントオクルージョン)マップ: 環境光の強さを表現する

他にもさまざまな用途で使われる。
用途が違うだけで、基本は各ピクセルにRGBが書き込まれている。
書き込まれたRGBの値をどう使うかによって名称が変わる。

法線マップ

法線マップはPS3あたりから登場。
目的はローポリで細かなディティールを表現するため。

細かい凹凸表現を頂点で表現すると極端にデータ量が増え、パフォーマンスに影響が出るため。
　…なのだが、UE5のNanite(ナナイト)機能によると法線マップが不要になる、らしい。

公式: https://www.unrealengine.com/ja/blog/a-first-look-at-unreal-engine-5
参考: https://soysoftware.sakura.ne.jp/archives/2314

し、知らなんだ…UEしゅごい…

実際の開発現場がどうなっているのかは分からないが、
UE専用で作る時やNaniteに制限がなければ本当に法線マップ不要だし、頂点数削減もLODも不要っぽい。

ただモデル単位で考えると、UE5以外の環境ではやはり従来のローポリモデルが必要なケースが多いため、完全にはなくならない、、と思う。

Unityにもくれんか？

法線マップの仕組み

目で凹凸を認識する時、最も重要なのは光の陰影。
この陰影の表現は、ライトの方向と頂点の法線によって決まっていた。（これまでに学習した内容）

つまり、法線の計算が出来さえすれば頂点がなくとも同様の陰影を表現することが可能という理論。
テクスチャのRGBに法線XYZを書き込むことで法線マップとして使える。

法線マップにはデータ形式によって次の2種類が存在する。

オブジェクトスペース法線マップ

オブジェクト空間の法線マップ。

法線が-1.0~1.0なのに対し、テクスチャRGBは0.0~1.0の範囲のため、
計算の際は (RGB値 – 0.5) * 2 で復元する。

この法線はオブジェクトの回転がかかっていない場合の法線のため、
使用する際はさらにワールド空間行列をかけてワールド空間に直してから使用する。

疑似コードは以下。

// オブジェクトスペース法線マップを読み込み
float3 normal = normalMap.Sample(sampler, In.uv).xyz;

// 復元
normal = (normal - 0.5f) * 2.0f;

// ワールド空間へ変換
normal = mul(worldMatrix, normal);

この方式だと法線マップテクスチャはモデル基準点からのベクトルになるためカラフルになる。
また変形の際に法線向きが固定されてしまい、意図しない法線になるため変形に弱い。
そのため、一般には使用されない。

タンジェントスペース法線マップ

法線マップを貼り付けるポリゴンの法線座標系から見た法線が書き込まれた法線マップ。
法線座標系は、以下の3つの直行するベクトルを規定軸とした空間のこと。

  • ポリゴンの法線ベクトル
  • 法線と直行している接ベクトル(タンジェントベクトル)
  • 法線と接ベクトルの外積で求めた従法線ベクトル

なおこの空間をタンジェントスペースとも呼ぶ。

タンジェントスペース補足

まｔｔｔｔｔったく分からなかったので調べた。

参考: https://coposuke.hateblo.jp/entry/2020/12/21/144327

タンジェントスペース(TBN空間)では、各RGB値は以下のように扱われる。

  • R = X = タンジェント方向(U方向)の成分
  • G = Y = バイノーマル方向(V方向)の成分
  • B = Z = 法線方向(垂直な長さ方向)の成分

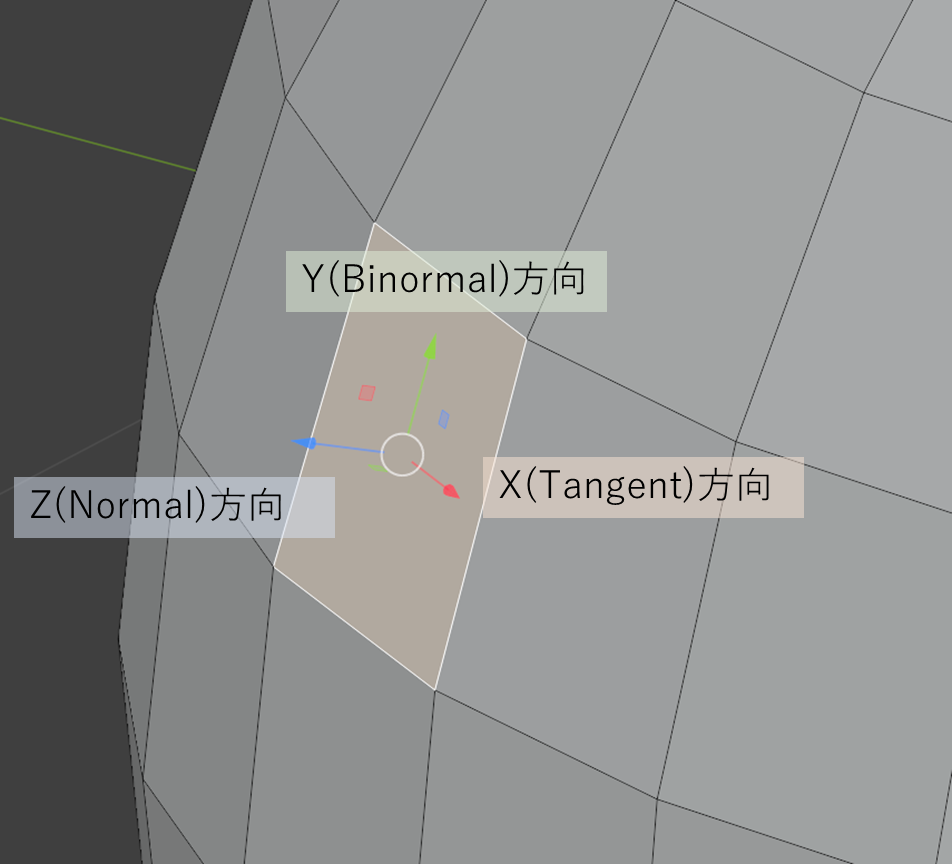
まず基準はメッシュ平面に垂直な法線である。
そのため、特に何も変更がない法線の場合、(0, 0, 1)になる。
これはUV方向に対し傾きがなく、メッシュに対して垂直なベクトルが法線に当たるためである。

次に、僅かにV方向に傾いた時の値を考えてみると、(0, 0.1, 0.995)となる。
法線は単位ベクトルのため、合成すれば必ず1となる。

これを逆手に取ったのがこの方法。
上記の場合、合成すれば僅かにV方向に傾くベクトルになることが分かる。

XY成分はUVであることから、メッシュのUV展開によって値が変わってくる。
オブジェクトスペースの場合は回転0の時を基準にしているためUVに影響されないが、TBNではこれを考慮する。
これにより、メッシュ変形によりポリゴン自体のTBNが変化したとしても、それに合わせて法線を再計算できるため常に正しい法線を得ることができる。

反対に、オブジェクトスペースの場合はメッシュが変形した際に法線マップの計算が合わなくなり、法線が崩れやすくなる。
これがTBNが原理的に変形に強い理由。

もう少し深堀をすると、
オブジェクトスペースはUV展開、メッシュの局所的な変形を考慮していない。

オブジェクト固有のローカル空間で表現されているため、例えば(0.7, 0, 0.7)の頂点に垂直な法線は(0.707, 0, 0.707)になるが、
この頂点が変形した時、面がどの方向に向いたのかを一つの行列から再計算することができない。

つまり、変形を考慮して法線を復元する際にTBNを使用するため、結果的に初めからTBNで保存した方が有利という見方ができる。

理論上はオブジェクトスペース法線マップから復元した法線をTBNに分解し、変形メッシュのTBN計算をすることで同様の結果を得ることができる、はず。

法線空間からワールド空間への変換

法線 * 基底軸 で求まる。

TBN空間における法線は各基底軸(メッシュから垂直なベクトル)が元になるため、これを掛けることでワールド空間にすることができる。

ワールド空間のベクトルをV、法線マップからのベクトルをVx,Vy,Vz、各頂点のTBN基底軸をT,B,Nとすると、以下の式で表すことができる。

V = (Vx * T) + (Vy * B) + (Vz * N)

TBN法線マップの場合、xyzの各成分はTBNに順ずるため、頂点からTBN情報を取得すれば復元することができる。

hlslで表すと以下の通り。

// 法線マップから読み込み
flaot3 localNormal = normalMap.Sample(sampler, In.uv).xyz;

// 復元
localNormal = (localNormal - 0.5f) * 2.0f;

// ワールド空間へ変換
float3 worldNormal = mul(localNormal, float3x3(tangent, binormal, normal));

この方式はメッシュから垂直なベクトル(Z方向に1なベクトル)が基準のため、
全体的にZ成分が多くなり青みがかる。

基本的にはこの方式が採用される。

実装

タンジェント、バイノーマルは頂点データのためセマンティクスで取得できる。
法線はNORMAL、接ベクトルはTANGENT、従ベクトルはBINORMALで取る。

struct SVSIn
{
    float4 pos : POSITION;  // モデルの頂点座標
    float3 normal : NORMAL; // 法線

    // step-1 頂点シェーダーの入力に接ベクトルと従ベクトルを追加
    float3 tangent : TANGENT;
    float3 binormal : BINORMAL;
};

法線適用前後。
適用後の方が細部の陰影がはっきりしているのが分かる。

スペキュラマップ

鏡面反射の強さを制限する。

例えば、1マテリアルで金属面と非金属面が共存するようなモデルで、
反射させたくない非金属面の箇所だけ黒く、金属面だけを白くすれば、反射箇所の制御ができる。

基本的にグレースケールのテクスチャになる。

実装

グレースケールのためRGBどの値を取得しても同じなため今回はR成分だけで判断。

float specPower = g_specularMap.Sample(g_sampler, psIn.uv).r;

反射光に直接掛ければ良いだけ。

specLig *= specPower

金属部分だけに鏡面反射が加わったことが分かる。

アンビエントオクルージョンマップ(AOマップ)

環境光の強さを制限する。

顎の下、首元など、環境光を受けやすい場所、受けにくい場所の環境光の強さを調整する。

大体はグレースケールのはず。

実装

テクスチャ読み込んで環境光に掛けるだけ。

float3 ambient = ambientLight;

// AOマップ読み込み
float ambientPower = g_aoMap.Sample(g_sampler, psIn.uv);

// 乗算
ambient *= ambientPower;

わずかに陰影がついたのが分かる。
この陰影を生み出すための光源調整を不要にし、意図した陰影をシンプルな環境光で表現するのが目的。

＼ 最新情報をチェック ／

コメント

PAGE TOP
タイトルとURLをコピーしました